CS PrimerAlgorithms and Data Structures
It is foolish to answer a question that you do not understand. It is sad to work for an end that you do not desire. George Polya Algorithms and Data Structures can be a particular rewarding area of study, because it drives at the core of computer programming: solving difficult problems.
In the course below, you’ll learn a number of important data structures and algorithms, which we’re sure will prove useful throughout your career. Just as importantly, you’ll develop a stronger ability to understand, break down and solve novel problems, whether inventing your own techniques or repurposing those which you learn here.
At the core of this course are the sequences of problems for each topic. You should aim to solve each problem, using the worked solutions and supplementary explainers as needed. For more suggestions on how to approach CS Primer, see the how-to guide.
Problem solving
In the words of Richard Hamming: "I have faith in only one [methodology] which is almost never mentioned—think before you write the program".From The Art of Doing Science and Engineering, best known for its inspiring chapter and corresponding lecture You and Your Research In this short warmup sequence, we practice actually thinking about technical problems, using a method modeled off George Pólya's How to Solve It.
Problems
| Staircase ascent FREE | crack a challenging programming problem using some techniques from Polya (31:06) |
| Convert to Roman | convert an integer to Roman numerals without a bunch of "if" statements (18:19) |
| Correct binary search | implement binary search without any edge case bugs using invariants (18:41) |
| Binary search revisited | reconsider binary search in a more flexible and powerful way (38:32) |
Explainers
Asymptotic analysis
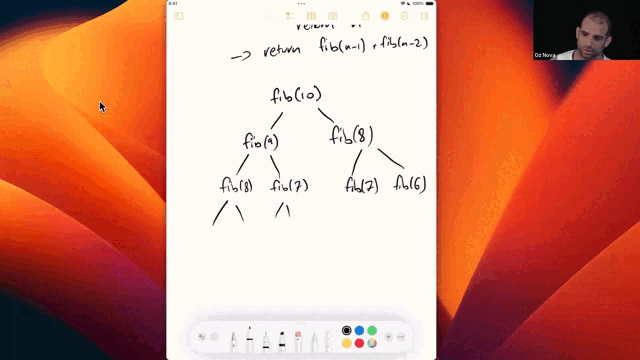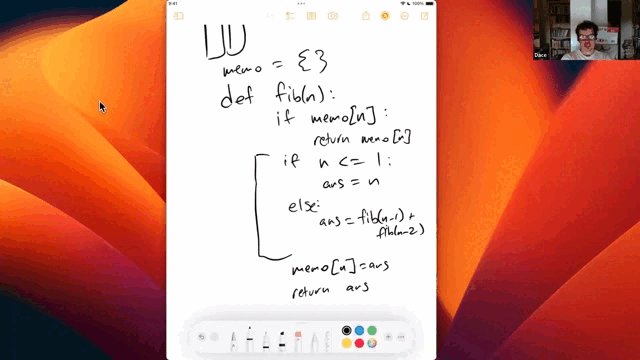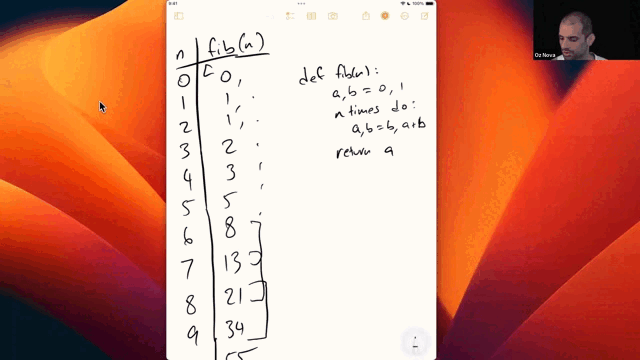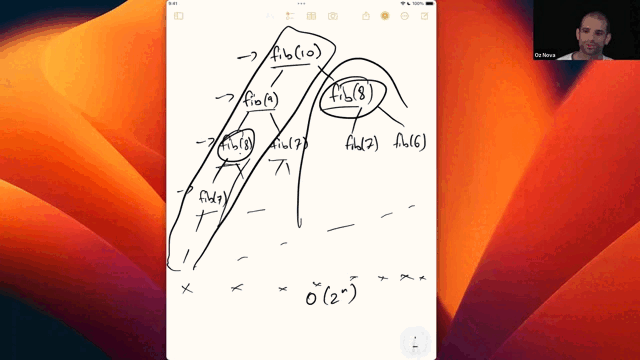
The analysis of algorithms is a huge field—to which some computer scientists dedicate their entire livesOne such devotee is Donald Knuth, who started writing The Art of Computer Programming in 1962 and has published approximately half of his planned volumes. but by the end of this module you should be able to assess the time and space cost, in Big O terms, of most of the programs you’ll encounter in the wild.
Expected release: November 2023
Dynamic arrays and linked lists
Most modern programming languages come with useful data structures built in, and it's particularly rare to see one without a dynamic array (known as a list in Python and simply "array" in JavaScript and Ruby). This module focuses on the power and flexibility of this humble structure, its specific use as a stack or queue, and some implementation considerations. We also cover linked lists as an occasionally useful alternative, and in preparation for our coverage of trees and graphs later.Consider that a tree is a special kind of graph where no node has more than one parent. A linked list is a special kind of tree where no node has more than one child.
Expected release: November 2023
Maps and sets
This module covers the particularly useful map data structure. While you may already be familiar with how to use maps, it's worthwhile to consider the various ways that they're implemented, so as to use them wisely and to borrow ideas!
Expected release: November 2023
Divide and conquer, and search algorithms
Divide and conquer is a broadly applicable problem solving strategy, renowned for producing astonishing results.One astonishing result is the Karatsuba algorithm for fast multiplication of two n-digit numbers. The renowned complexity theorist Kolmogorov had conjenctured that the fastest possible multiplication algorithm was O(n2), and presented this conjecture at a seminar in 1960 attended by the then 23-year-old Karatsuba. Within a week, Karatsuba had disproved the conjecture, finding an O(nlog23) algorithm using an approach which would later come to be named divide and conquer.
This caused Kolmogorov to become wildly excited, terminating the seminar series and publishing and article on the result in Karatsuba’s name, kick starting a period of intense interest in the area.
The history of the result is detailed in Karatsuba’s later paper The Complexity of Computations. Pictured below is Karatsuba as a high school graduate, a few years before his remarkable discovery.
We’ll explore the idea generally, as well as in the context of sorting. Here we’ll explore the problem until we’re convinced that it can be done at no better than O(n2), and be duly impressed by two divide and conquer based algorithms that manage to run at the much better O(n log n)! It’s uncommon—though a rare pleasure—to implement your own sorting algorithms from scratch, so instead we’ll focus our discussion on the overall strategy, as it can be applied in main domains outside of searching and sorting.
Expected release: December 2023
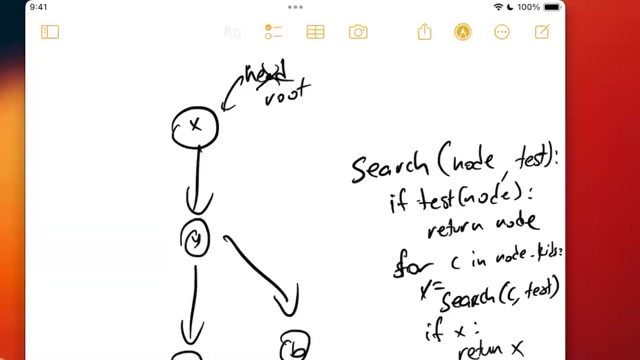
Tree traversal and graph search
If we had to choose a single Greatest Hit of algorithms, it would be graph search. It’s tempting to give examples where graph search shines,The stereotypical examples are social networks, the web and the internet. But if we were to emphasize these examples, you’re likely to come away with a narrow view of what is in fact a very broadly applicable tool. but by the end of this module you’ll actually appreciate that almost anything can be modeled as a graph and almost any problem can be solved with graph search.
In this module we’ll start with simple breadth first and depth first traversal over trees, and extend our understanding to breadth first search and depth first search over unweighted graphs. By the end, you should be able to confidently choose between these two strategies, and implement either one over graphs that you model yourself.
Expected release: December 2023
Weighted graphs, Dijkstra’s algorithm and A*
Breadth-first and depth-first search are tremendously useful, but don’t quite extend to finding shortest path over weighted graphs,Recall that a weighted graph is one where the strength of the relationship between two entities matters, which we model by assigning a “weight” value to edges. which turns out to be a common problem. 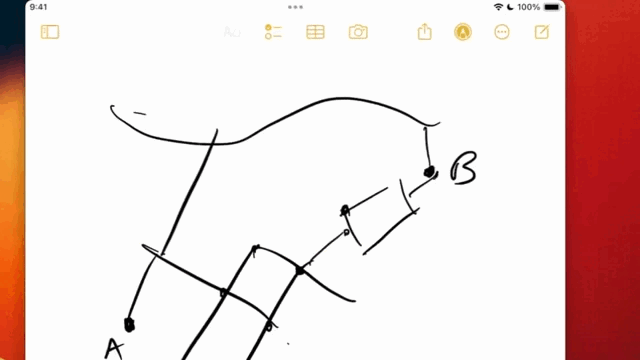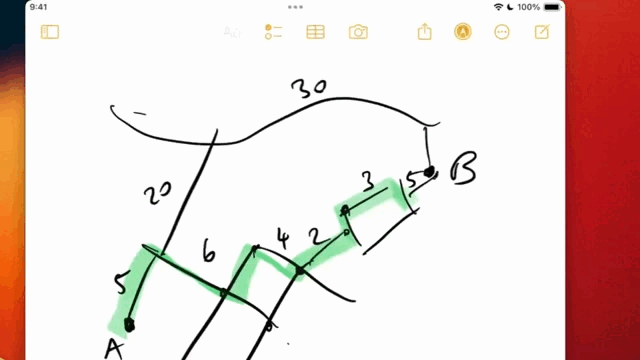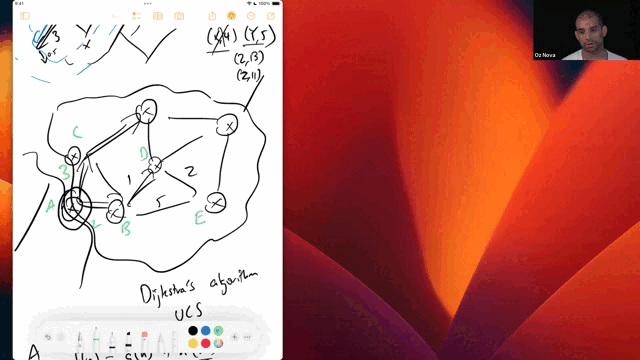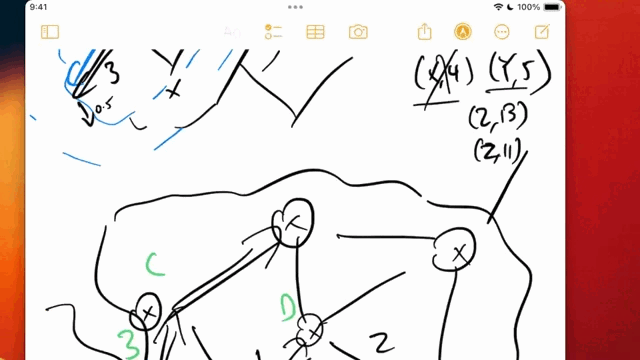In this module, we develop our understanding of graph search further with with two important algorithms: Dijkstra’s algorithmWhile we stick with the convention of calling this algorithm Dijkstra’s, the better name—used more in the AI community—is “uniform cost search”. Dijkstra was the first to develop many algorithms, but this one was well known to others before Dijkstra re-discovered it. Furthermore, “uniform cost search” begins to describe its approach: the frontier of the search is defined by points of equivalent cost. and A*.Pronounced “A-star”, this algorithm was developed at Stanford Research Institute to help Shakey the Robot navigate obstacles in a room. At the time, Dijkstra’s algorithm was the best path planning option available. A* was seen as a minor enhancement to the algorithm, but the improvement in efficiency was very significant.
Pictured below is Shakey on display at Computer History Museum.
Using A* search in practice is all about finding suitable “heuristic functions”, which are measures of how close we are to our goal. We’ll practice this skill on problems where the choice of heuristic function makes a significant difference.
Expected release: December 2023
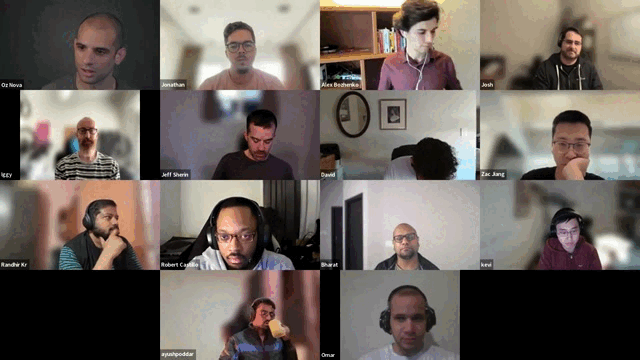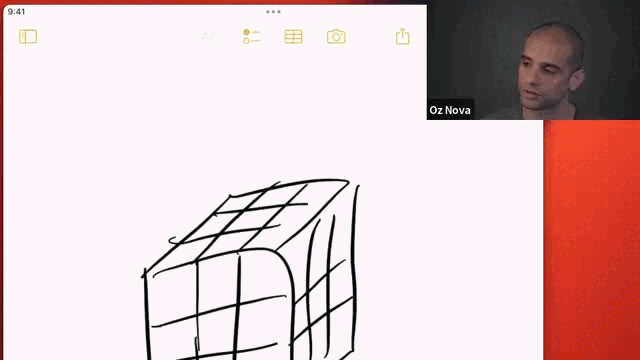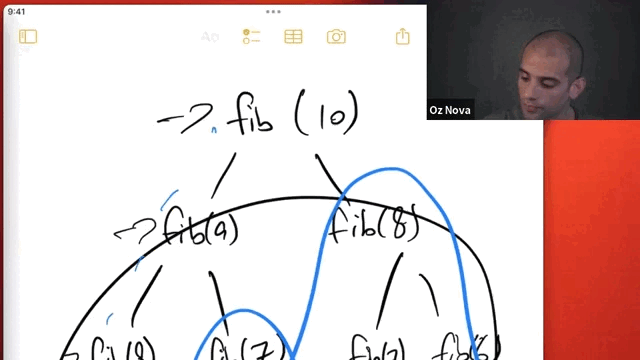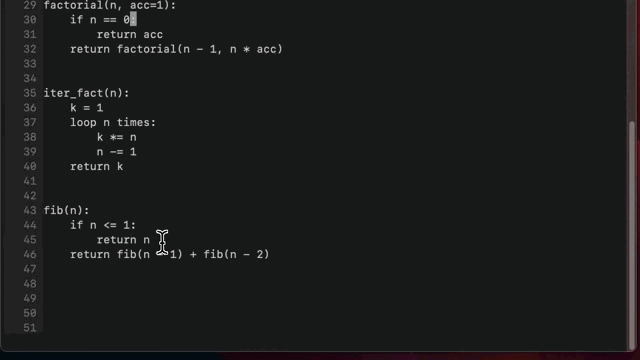
Dynamic programming
This class ensures that your recursive thinking is not in vain, by introducing dynamic programming: an important technique to avoid unnecessary computation and render certain recursive problems tractable.The name “dynamic programming” could certainly be more descriptive. Richard Bellman claims in his autobiography that he chose these words because it’s impossible to use the adjective “dynamic” in a pejorative sense, and because the practical connotation of the word “programming” would appeal to the research-averse Secretary of Defense of the time (who was indirectly responsible for his funding).
This story may not quite be true; an alternative account suggests that he was trying to “upstage Dantzig’s linear programming by adding dynamic”. For more, see the dynamic programming Wikipedia article. Dynamic programming has proved invaluable in applications varying from database query optimization to sequence alignment in bioinformatics.
Expected release: December 2023